Java Generalized Suffix Tree
Years ago, I researched Generalized Suffix Trees as part of solving a programming challenge in order to apply for a job I was interested in. I needed to build an app featuring instant ($\lt 0.1 ms$) search capability over a fairly large set of strings.
I discovered generalized suffix trees could help me achieve my goal. However, when I looked for existing implementations in Java and could not find any, I ended up writing my own.
A year later, when the original programming puzzle had been retired, I decided to publish my Generalized Suffix Tree implementation on GitHub as Open Source and document what I had learned.
Suffix Trees
Suffix trees are powerful data structures offering fast operations when working with strings, based on the intuition of constructing a compact trie containing all the suffixes contained in a given input string and using that as an index for lookup operations.
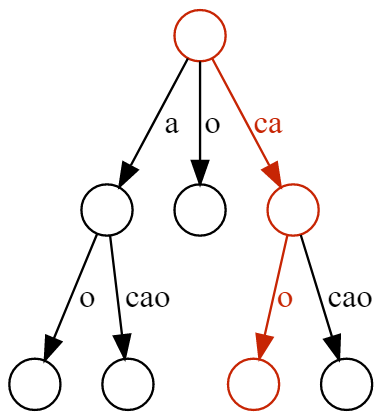
cacao. A suffix is said to be contained in the tree if there is a path from the root node where the string obtained by concatenating the edge labels has the same prefix as the suffix being looked up. Highlighted the path corresponding to the cao suffix.One of the most common use cases is locating a substring (of assumed length $m$) within a much longer string (of length $n$), which can be done with running time $O(m)$. In most applications, $m \ll n$, so suffix trees present a clear advantage over simply scanning the longer string until a match is found.
As a concrete frame of reference, the human genome can be encoded as a 3GB string constructed out of an alphabet of four characters, each representing a specific nucleotide (canonically encoded as one of A, C, G, T), therefore many problems in computation biology can make good use of data structures providing fast string sequence lookup.
Building and storing suffix trees is costly: the trees themselves tend to require much more memory than the string they are indexing. As of 2019, a suffix tree indexing the human genome using state of the art algorithms can easily occupy tens of gigabytes.
Ukkonen introduced an algorithm capable of constructing a suffix tree in $O(n)$ runtime for a constant-size alphabet and $O(n \log n)$ worst-case running time, a significant improvement to the preceding work which often required $O(n^2)$ runtime. A couple years later Farach proposed an alternative approach that is optimal for all alphabets.
Runtime cost of the construction phase does matter because suffix trees are commonly used to index very large strings, such as in computational biology – where they are used to manipulate DNA sequences encoded as strings – or text editing and processing.
Generalized Suffix Trees
A generalized version of the data structure described above can be used to index multiple strings. In this case, the result of a search operation could be a reference to which string(s) contain a given input string.
In literature, the problem of working with Generalized trees is often reduced to the well researched problem of working with a more traditional suffix tree by introducing a set of special terminator symbols and assuming that each word is terminated with a unique terminator suffix.
Therefore, the problem of building a generalized suffix tree over words $w_1$, $w_2$ and $w_3$, where
$\begin{align*}
w_1 &= abcd\\
w_2 &= efg\\
w_3 &= hijk
\end{align*}$
can be reduced to the problem of building a suffix tree for the string $s = abcd {\color{red} \alpha} efg {\color{red} \beta} hijk {\color{red} \gamma}$, where $\alpha$, $\beta$ and $\gamma$ are the terminator strings we use to separate the strings we want to index.
While this has many advantages (it allows to cleanly generalize proofs, algorithms and papers), it does not scale very well (because of the requirements for the terminator strings to be unique) and, even if it did, it would make for bulky implementations. In practice, most implementations are built differently and embed additional information in the tree nodes to encode references to the different strings.
Implementation Considerations
The code in this library generalizes the algorithm described in Ukkonen’s paper On-line construction of suffix trees so that it works with multiple strings (the original paper was written for the use case of indexing a single large string).
The resulting data structure retains the key performance characteristics that make suffix trees appealing. Namely, assuming we are working with a set of strings $D = {S_1, S_2, …, S_k}$ of total length $n = n_1 + n_2 + … + n_k$:
- the runtime cost of building the tree is $O(n)$
- the runtime cost of looking up a string $P$ or length $m$ is $O(m)$
However, being a generalized tree built out of multiple strings, when looking up $P$, we can retrieve multiple matches, one for each string $S_i$ of which $P$ is a substring.
The core of the library is a
GeneralizedSuffixTree class, offering a simple interface supporting search and put operations and implementing the suffix tree data structure by relying on ancillary classes representing Nodes and Edges. The implementation retains some optimizations (listed below) specific to the problem I was trying to solve as I wrote it I had to make to respect the memory constraints tied to my original challenge but is general purpose enough that can be used for other applications too.
Problem-specific optimizations
The use case I wrote this for was to index a given set of ASCII strings under a limited memory budget, optimizing for fast lookup times. This resulted into leveraging some of these assumptions to achieve a smaller memory footprint and more efficient lookups. Also, my use case was focused just on determining which strings contained a given suffix and did not need to return the position for the match. Therefore, I simplified the implementation by not storing positional indexes.
Most of these optimizations are encapsulated in the
Node and
EdgeBag classes and revolve around the library being optimized for the ASCII alphabet.
Node maintains a set of outgoing edges indexed by a character (the next character in the suffix stored in the subtree rooted in the given node), represented as an EdgeBag.
EdgeBag is functionally a Map<Character, Edge> with a few tweaks to make it more compact than a HashMap or TreeMap:
- It uses arrays of native types instead of boxed types.
- It uses
bytevariables to represent characters. This leads to memory savings for ASCII trees but does not scale well to handle Unicode alphabets where characters might need to be represented with more than a single byte. - Instead of using a hash table (implying memory overhead at low load factors) or a tree map (implying memory overhead because of the need to represent nodes and links between them) for mapping characters to edges,
EdgeBagrelies on two parallel arrays of sorted size, one reserved for the keys and another for the values. At small sizes, a lookup is implemented by sequentially scanning the keys array to find a match. WhenEdgeBag’s side exceeds a cutoff size (empirically set to 6 in my case), relying on sorting they keys and binary search on lookup is faster. For my data set, the vast majority of instances were small and binary search was rarely used.
If you need to work with larger character sets (Java supports Unicode), you can replace the EdgeBag reference
here and work with a plain HashMap instead.